Tiempo de Duplicación. El denominado tiempo de duplicación "Tau" es uno de los indicadores más básicos para seguir la evolución de una epidemia. También es el más problemático para interpretar, porque su definición se basa en la hipótesis de un permanente crecimiento exponencial del número de casos acumulados. Tal hipótesis es sólo válida en poblaciones grandes, homogéneas, con gente muy mezclada. En la práctica existe una superposición de brotes provocando aumentos y disminuciones del número de casos diarios, y aunque el número de casos positivos acumulados crezca monótonamente, el modelo exponencial aplicado en una ventana de tiempo no es necesariamente el más adecuado para describirlos.

Modelo SIR. El crecimiento exponencial del número de casos acumulados suele justificarse con modelos muy sencillos como el modelo SIR en la etapa de crecimiento, cuando la fracción de susceptibles es alta y puede considerarse una constante S0 en el tiempo de obervación. Si I(t) es la cantidad de infectados a tiempo t, en el modelo SIR tenemos

dI/dt = beta S0 I - gamma I

donde beta es la frecuencia de contagio y gamma la de recuperación, o inversas de los tiempos característicos de contagio y recuperación. Si beta, gamma y S0 se mantienen constantes en un intervalo dt alrededor de t tenemos que,

I(t) = I(t-dt) exp[(beta S0 - gamma) dt] = I(t-dt) exp[gamma(R0 S0 - 1) dt]

donde R0 es el número de reproducción básico. Escribiendo

I(t) = I(t-dt) 2^{dt/Tau} = I(t-dt) exp[log(2) dt/Tau]

vemos que

Tau = log(2)/[gamma(R0 S0 - 1)]

de modo que Tau>0 solo si R0 S0 > 1. Esta última es la condición fundamental para el inicio de una epidemia en una población susceptibles.

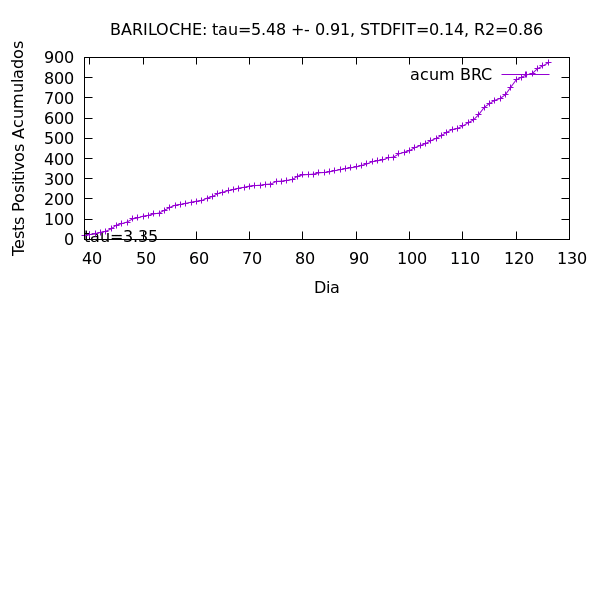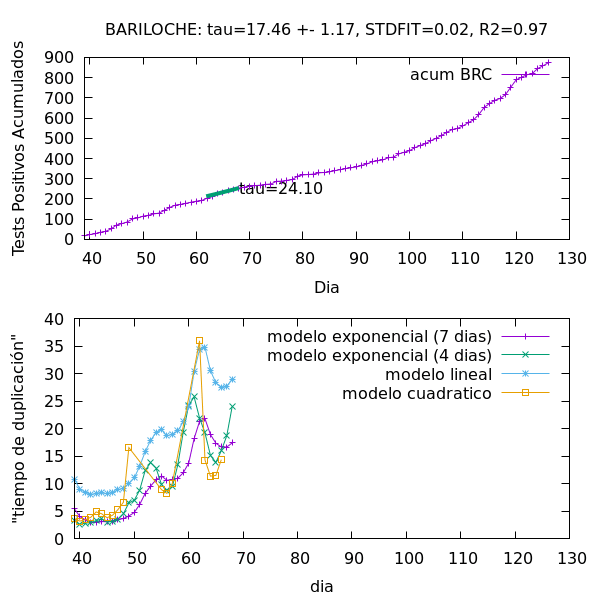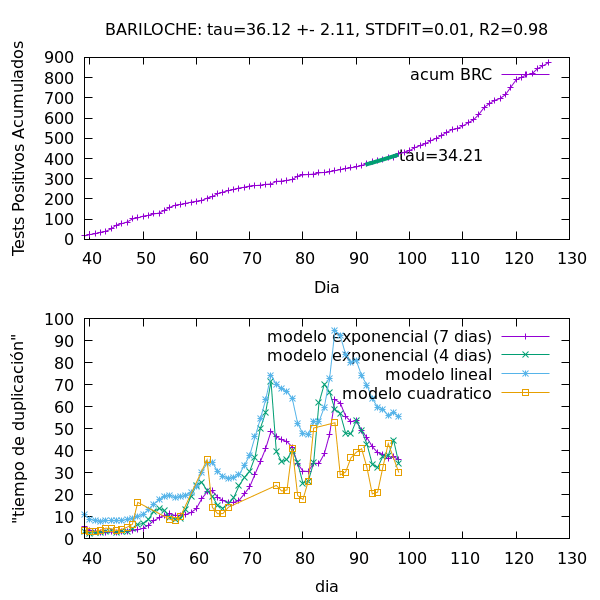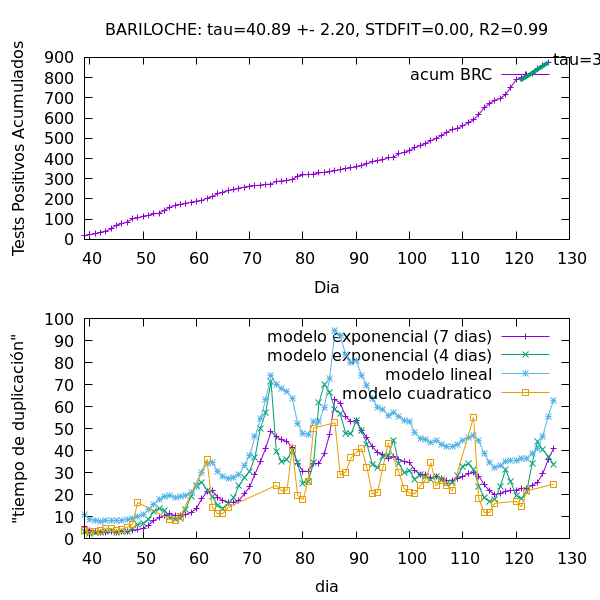
Procedimiento Numérico. El procedimiento que por ejemplo usa el ministerio de Salud de la Nación para calcularlo es el de ajustar al número acumulado de casos A(t) un crecimiento exponencial del tipo A(t)=A(t-dt) 2^{dt/Tau} en una ventana de siete días para atrás, es decir en el intervalo [t-7,t]. En la práctica se hace un ajuste lineal a log[A(t)] en la misma ventana y de allí se extrae Tau ~ log(2)/[dlog(A)/dt]. Ver animación de ejemplo para Bariloche de este procedimiento, en el primer panel.

El problema de la heterogeneidad. Como se muestra en la animación del primer panel, es evidente que el mismo ajuste se puede hacer con polinomios de bajo orden, y muchas veces con uno lineal. De hecho la bondad del ajuste es a menudo mejor para modelos no exponenciales. Esto atenta contra la propia definición de Tau, ya que un ajuste lineal o polinómico por ejemplo, es sólo consistente con Tau=infinito en la definición original del modelo de crecimiento puramente exponencial. Notar que al ser el número de casos acumulados monótonamente creciente, Tau está restringido a ser positivo, siendo infinito cuando la epidemia cesa. Si reinterpretamos Tau como una extrapolación que dobla el número de casos para el mejor modelo de ajuste, Tau daría un valor mucho más grande que la aproximación exponencial. En el panel inferior de la animación se ven los distintos "tiempos de duplicación" qeu podrian definirse, y como deciamos anteriormente, ninguno es mejor modelo de ajuste que otro. En este sentido el error del tiempo de duplicación es por tanto grande.

Demoras. Los casos primarios positivos hoy producirán casos secundarios no hoy mismo, sino en un intervalo mas o menos definido de días, de modo que una aproximación más aceptable para estimar la tasa de crecimiento de la epidemia es un estimador del Número de Reproducción Empírico, más que del tiempo de duplicación. Esta es una primera motivación para introducir esta cantidad en nuestro diagrama de Riesgo. La segunda motivación, es que si conocemos el número de casos activos hoy, el número de reproducción empírico nos permite hacer una predicción de corto plazo del número de casos en los próximos días. Una predicción así es útil para saber si el sistema sanitario está preparado para contenerlos.

Dos variables. Si bien sigue siendo una super-simplificación, describir la evolución global de la epidemia con dos indicadores relacionados (el Número de Reproducción Empírico y la Tasa de Ataque o Incidencia), ambos basados en el número de casos diarios, nos permite apreciar mucho mejor la complejidad de la epidemia que solo usar el tiempo de duplicación. El diagrama de riesgo es por tanto una forma mas fina de capturar la dinámica de la epidemia.